投資者經常會遇到這樣一個問題,買到一隻股票上漲後,後悔自己買少瞭,當初應該全倉,甚至借錢買入的,特別當股票漲幅較大時;買到一隻股票下跌後,悔恨自己買多瞭,要是當初沒買該多好,特別是跌幅較大時。可是,人非神,誰能每次買入股票後都上漲呢,即使是索羅斯、彼得林奇這種大神也做不到。
炒股有時掙、有時虧,這是常態。如何分配資金,保證最終掙的比虧的多,最高效率的積累長期資金呢?凱利公式就是解決這個問題的。
我們先看一下凱利公式:f=(b*p-q)/b,其中f表示每次投入的資產比例,b為盈虧比,b=平均盈利金額/平均虧損金額;p為勝率,q為虧損概率,p+q=1。凱利公式的證明過程如下:

呵呵呵,感興趣的朋友請自行私下研究,繁復的證明過程還是省略吧。
假設:勝率p=0.6,盈虧比b=1.3。盈利的期望值為0.38,為正值,即有利可圖。假設初始金額為1,初始倉位為0.1至1.9f,利用凱利公式計算的倉位為0.1倍至2倍。交易200次以後,最終資金數額如下圖所示:
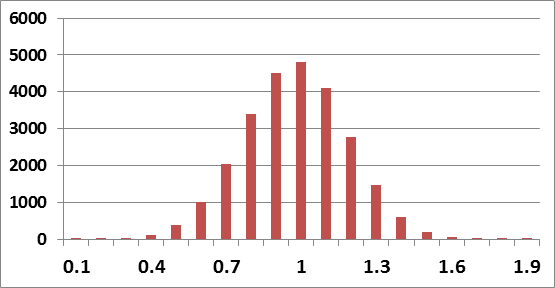
其中橫坐標為倉位。根據該圖我們可以看到,此種情況下,當f=1時,獲利金額最大。
由此,我們可以得到這樣的啟示,在此種勝率與盈虧比的情況下,每次可全額投入,可以獲得最大額度的利潤。但不要借錢炒股,這時候借錢並不能讓你獲得更高效的收益。
有人做過驗算,當期望值相同時,即b*p-q相同時,勝率越大,盈虧比越小,f越大。在期望值相同時,資金增長率隻與單次下註額有關。所以當勝率較高時,可以提高每次投入的資金量。這與我們的直觀感受也是一致的。
根據b*p-q,提高盈虧比b,即每次掙的錢遠多於虧的錢,即使虧的次數多於掙的次數,也是能掙錢的。

當然,現實運用中,由於p與b是變動的,不同的市場情況不一樣,不同的投資人特質不一樣,凱利公式並不容易應用。可以根據不同的情況,采用不同的策略。拾荒網,一個有價值的炒股知識學習網站。